有位同学的代码体现了c的性质,研究了一会儿,这里不得不发个朋友圈说一下了
现在有如下几个问题:
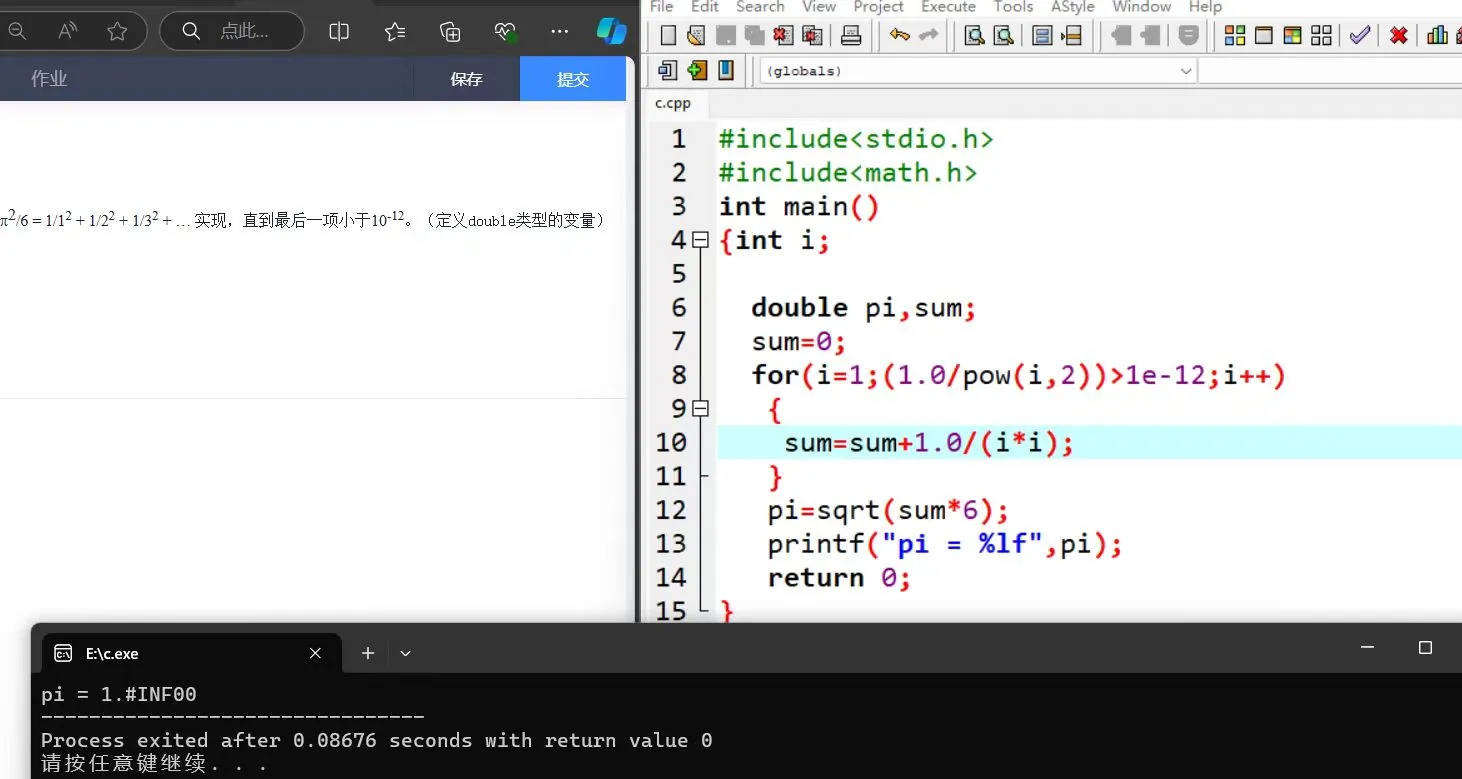
- 图中代码 i * i 改为 pow(i, 2) 时,程序正常输出,π更精确,但是当 pow(i, 2) 改为 i * i 时,程序正常输出,π不太精确。(使用 pow(i, 2) 无法正确实现题目效果)
- 为什么不修改图中代码,输出1.#INF00?
对于问题一:
pow 内部是采用 double 类型计算数的平方,double数容纳范围更广,所以更精确。而 i * i 计算平方,只是进行int整数相乘,所以不如 pow 精确,还会导致溢出问题。
对于问题二:
1.#INF00 是无穷大的意思,一般是除数为零导致的。
导致这个问题原因是,pow(i, 2) 过于精确,使得 pow(i, 2) <= 1e-12 迟迟不成立,循环一直进行,次数甚至超过了 65536 次。
虽然 sum = sum + 1.0 / (i * i) 时,用了 1.0 ,编译器应该会将数据类型转化为 double,但是由于 i * i 被括号括起来了,先进行计算,i * i 的结果仍然是 int 类型。
int 类型在操作系统中一般占 32 位,最大值是2,147,483,647,最小值是-2,147,483,648,(一共存的下4,294,967,296个数)。
由于循环次数达到 65536 次,
理论上会计算出
65536*65536=4,294,967,296(刚好是int类型存得下的数的数量)
但是很明显这个数int类型存不下(最大能存的整数也只是它的一半),所以只好采取溢出的方式。即溢出为 0。
导致变成 1.0 / 0 = 1.#INF00 (无穷大),使最后结果不正确。
这个bug体现了:c语言中的迷惑类型转换和神奇的溢出
我的评价是:不如 Python